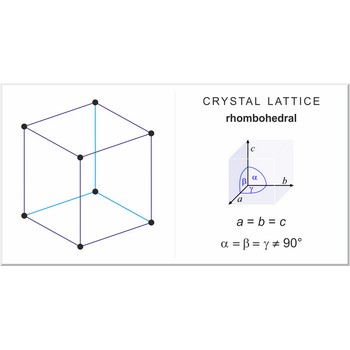
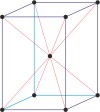
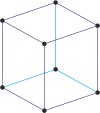
rhombohedral lattice → romboedarska rešetka
Rhombohedral (or trigonal) lattice has one lattice point at the each corner of the unit cell. It has unit cell vectors a=b=c and interaxial angles α=β=γ≠90°.
Bravais lattice → Bravaisova rešetka
Bravais lattice is a set of points constructed by translating a single point in discrete steps by a set of basis vectors. The French crystallographer Auguste Bravais (1811-1863) established that in three-dimensional space only fourteen different lattices may be constructed. All crystalline materials recognised till now fit in one of these arrangements. The fourteen three-dimensional lattices, classified by crystal system, are shown to the bottom.
|
Crystal system
|
Bravais lattices
|
|||
|
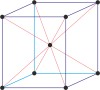
cubic a=b=c α=β=γ=90° |
 |
 |
 |
|
|
|
simple cubic
|
body-centered cubic
|
face-centered cubic
|
|
|
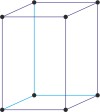
tetragonal a=b≠c α=β=γ=90° |
 |
 |
||
|
|
simple tetragonal
|
body-centered tetragonal
|
||
|
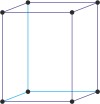
orthorhombic a≠b≠c α=β=γ=90° |
 |
 |
 |
 |
|
|
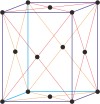
simple orthorhombic
|
base-centered orthorhombic
|
body-centered orthorhombic
|
face-centered orthorhombic
|
|
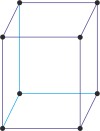
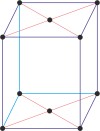
monoclinic a≠b≠c α=γ=90°≠β |
 |
 |
||
|
|
simple monoclinic
|
base-centered monoclinic
|
||
|
hexagonal a=b≠c α=β=90° γ=120° |
 |
|||
|
|
hexagonal
|
|||
|
rhombohedral a=b=c α=β=γ≠90° |
 |
|||
|
|
rhombohedral
|
|||
|
triclinic a≠b≠c α≠β≠γ≠90° |
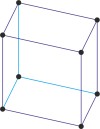 |
|||
|
triclinic
|
||||
base-centered monoclinic lattice → bazno centrirana monoklinska rešetka
Base-centered or side-centered or end-centered monoclinic lattice (monoclinic-C), like all lattices, has lattice points at the eight corners of the unit cell plus additional points at the centers of two parallel sides of the unit cell. It has unit cell vectors a≠b≠c, and interaxial angles α=γ=90°≠β.
base-centered orthorhombic lattice → bazno centrirana ortorompska rešetka
Base-centered or side-centered or end-centered monoclinic lattice (orthorhombic-C), like all lattices, has lattice points at the eight corners of the unit cell plus additional points at the centers of two parallel sides of the unit cell. It has unit cell vectors a≠b≠c and interaxial angles α=β=γ=90°.
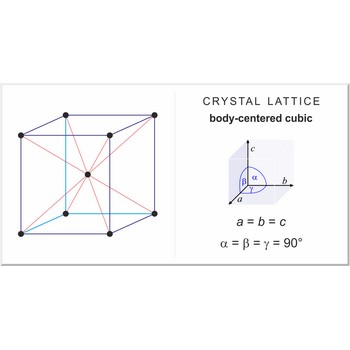
body-centered cubic lattice → prostorno centrirana kubična rešetka
Body-centered cubic lattice (bcc or cubic-I), like all lattices, has lattice points at the eight corners of the unit cell plus an additional points at the center of the cell. It has unit cell vectors a = b = c and interaxial angles α=β=γ=90°.
The simplest crystal structures are those in which there is only a single atom at each lattice point. In the bcc structures the spheres fill 68 % of the volume. The number of atoms in a unit cell is two (8 × 1/8 + 1 = 2). There are 23 metals that have the bcc lattice.
body-centered orthorhombic lattice → prostorno centrirana ortorompska rešetka
Body-centered orthorhombic lattice (orthorhombic-I), like all lattices, has lattice points at the eight corners of the unit cell plus an additional points at the center of the cell. It has unit cell vectors a≠b≠c and interaxial angles α=β=γ=90°.
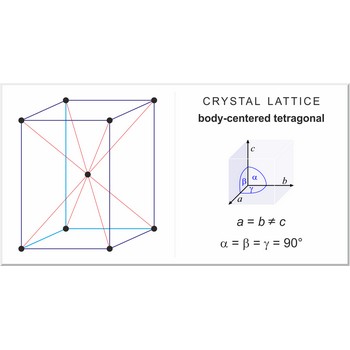
body-centered tetragonal lattice → prostorno centrirana tetragonska rešetka
Body-centered tetragonal lattice (tetragonal-I), like all lattices, has lattice points at the eight corners of the unit cell plus an additional points at the center of the cell. It has unit cell vectors a=b≠c and interaxial angles α=β=γ=90°.
lattice → kristalna rešetka
Crystal lattice is a three-dimensional array of points that embodies the pattern of repetition in a crystalline solid. Don’t mix up atoms with lattice points: lattice points are infinitesimal points in space - atoms are physical objects.
lattice constants → konstante kristalne rešetke
Lattice constants are parameters specifying the dimensions of a unit cell in a crystal lattice, specifically the lengths of the cell edges and the angles between them.
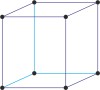
face-centered cubic lattice → plošno centrirana kubična rešetka
Face-centered cubic lattice (fcc or cubic-F), like all lattices, has lattice points at the eight corners of the unit cell plus additional points at the centers of each face of the unit cell. It has unit cell vectors a =b =c and interaxial angles α=β=γ=90°.
The simplest crystal structures are those in which there is only a single atom at each lattice point. In the fcc structures the spheres fill 74 % of the volume. The number of atoms in a unit cell is four (8×1/8 + 6×1/2 = 4). There are 26 metals that have the fcc lattice.
Citing this page:
Generalic, Eni. "Rhombohedral lattice." Croatian-English Chemistry Dictionary & Glossary. 29 June 2022. KTF-Split. {Date of access}. <https://glossary.periodni.com>.
Glossary
Periodic Table