CHEMISTRY GLOSSARY

Bravais lattice is a set of points constructed by translating a single point in discrete steps by a set of basis vectors. The French crystallographer Auguste Bravais (1811-1863) established that in three-dimensional space only fourteen different lattices may be constructed. All crystalline materials recognised till now fit in one of these arrangements. The fourteen three-dimensional lattices, classified by crystal system, are shown to the bottom.

Crystal system	Bravais lattices
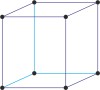
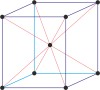
cubic a=b=c α=β=γ=90°
	simple cubic	body-centered cubic	face-centered cubic
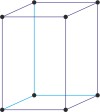
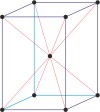
tetragonal a=b≠c α=β=γ=90°
	simple tetragonal	body-centered tetragonal
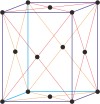
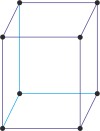
orthorhombic a≠b≠c α=β=γ=90°
	simple orthorhombic	base-centered orthorhombic	body-centered orthorhombic	face-centered orthorhombic
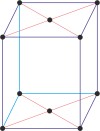
monoclinic a≠b≠c α=γ=90°≠β
	simple monoclinic	base-centered monoclinic
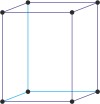
hexagonal a=b≠c α=β=90° γ=120°
	hexagonal
rhombohedral a=b=c α=β=γ≠90°
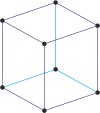	rhombohedral
triclinic a≠b≠c α≠β≠γ≠90°
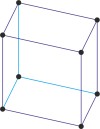	triclinic