CHEMISTRY GLOSSARY

vertical ionisation energy    →   vertikalna energija ionizacije

Vertical ionisation energy is the energy required to remove an electron from an atom, molecule, or ion in the gas phase without moving any nuclei. The vertical ionisation energy is greater than or equal to the adiabatic ionisation energy.

Gibbs free energy    →   Gibbsova slobodna energija

Gibbs free energy (G) is an important function in chemical thermodynamics, defined by

where H is the enthalpy, S the entropy, and T the thermodynamic temperature. Gibbs free energy is the energy liberated or absorbed in a reversible process at constant pressure and constant temperature. Sometimes called Gibbs energy and, in older literature, simply free energy.

Changes in Gibbs free energy, ΔG, are useful in indicating the conditions under which a chemical reaction will occur. If ΔG is negative the reaction will proceed spontaneously to equilibrium. In equilibrium position ΔG = 0.

kinetic energy    →   kinetička energija

Kinetic energy (E_k) is associated with the state of motion of a body. It is a scalar property and defined to be

Kinetic energy is most clearly exhibited in gases, in which molecules have much greater freedom of motion than in liquids and solids.

potential energy    →   potencijalna energija

Potential energy (E_p) is the energy stored in a body or system as a consequence of its position, shape, or state (this includes gravitation energy, electrical energy, nuclear energy, and chemical energy). Gravitational potential energy is the energy associated with the state of separation between bodies that attracts each other via gravitational force. Elastic potential energy is the energy associated with the state of compression or extension of an elastic object. Thermal energy is associated with the random motions of atoms and molecules in a body.

Bravais lattice    →   Bravaisova rešetka

Bravais lattice is a set of points constructed by translating a single point in discrete steps by a set of basis vectors. The French crystallographer Auguste Bravais (1811-1863) established that in three-dimensional space only fourteen different lattices may be constructed. All crystalline materials recognised till now fit in one of these arrangements. The fourteen three-dimensional lattices, classified by crystal system, are shown to the bottom.

Crystal system	Bravais lattices
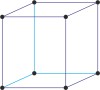
cubic a=b=c α=β=γ=90°
	simple cubic	body-centered cubic	face-centered cubic
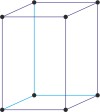
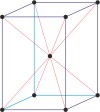
tetragonal a=b≠c α=β=γ=90°
	simple tetragonal	body-centered tetragonal
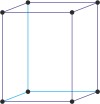
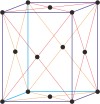
orthorhombic a≠b≠c α=β=γ=90°
	simple orthorhombic	base-centered orthorhombic	body-centered orthorhombic	face-centered orthorhombic
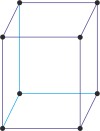
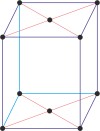
monoclinic a≠b≠c α=γ=90°≠β
	simple monoclinic	base-centered monoclinic
hexagonal a=b≠c α=β=90° γ=120°
	hexagonal
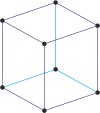
rhombohedral a=b=c α=β=γ≠90°
	rhombohedral
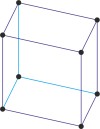
triclinic a≠b≠c α≠β≠γ≠90°
	triclinic

base-centered monoclinic lattice    →   bazno centrirana monoklinska rešetka

Base-centered or side-centered or end-centered monoclinic lattice (monoclinic-C), like all lattices, has lattice points at the eight corners of the unit cell plus additional points at the centers of two parallel sides of the unit cell. It has unit cell vectors a≠b≠c, and interaxial angles α=γ=90°≠β.

base-centered orthorhombic lattice    →   bazno centrirana ortorompska rešetka

Base-centered or side-centered or end-centered monoclinic lattice (orthorhombic-C), like all lattices, has lattice points at the eight corners of the unit cell plus additional points at the centers of two parallel sides of the unit cell. It has unit cell vectors a≠b≠c and interaxial angles α=β=γ=90°.

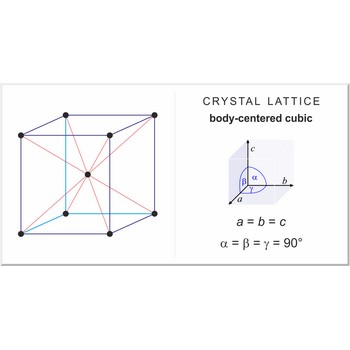
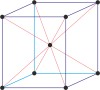
body-centered cubic lattice    →   prostorno centrirana kubična rešetka

Body-centered cubic lattice (bcc or cubic-I), like all lattices, has lattice points at the eight corners of the unit cell plus an additional points at the center of the cell. It has unit cell vectors a = b = c and interaxial angles α=β=γ=90°.

The simplest crystal structures are those in which there is only a single atom at each lattice point. In the bcc structures the spheres fill 68 % of the volume. The number of atoms in a unit cell is two (8 × 1/8 + 1 = 2). There are 23 metals that have the bcc lattice.

body-centered orthorhombic lattice    →   prostorno centrirana ortorompska rešetka

Body-centered orthorhombic lattice (orthorhombic-I), like all lattices, has lattice points at the eight corners of the unit cell plus an additional points at the center of the cell. It has unit cell vectors a≠b≠c and interaxial angles α=β=γ=90°.

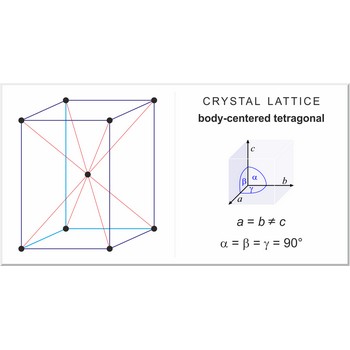
body-centered tetragonal lattice    →   prostorno centrirana tetragonska rešetka

Body-centered tetragonal lattice (tetragonal-I), like all lattices, has lattice points at the eight corners of the unit cell plus an additional points at the center of the cell. It has unit cell vectors a=b≠c and interaxial angles α=β=γ=90°.