Results 1–5 of 5 for tetragonal
body-centered tetragonal lattice → prostorno centrirana tetragonska rešetka
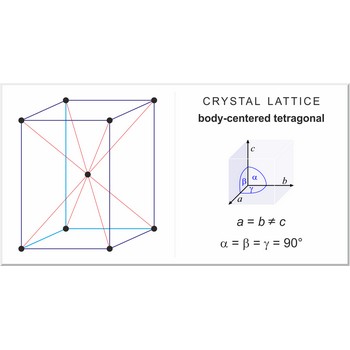
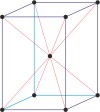
Body-centered tetragonal lattice (tetragonal-I), like all lattices, has lattice points at the eight corners of the unit cell plus an additional points at the center of the cell. It has unit cell vectors a=b≠c and interaxial angles α=β=γ=90°.
simple tetragonal lattice → jednostavna tetragonska rešetka
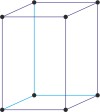
Simple or primitive tetragonal lattice (tetragonal-P) has one lattice point at the each corner of the unit cell. It has unit cell vectors a=b≠c and interaxial angles α=β=γ=90°.
tetragonal crystal system → tetragonski kristalni sustav
Minerals of the tetragonal crystal system are referred to three mutually perpendicular axes. The two horizontal axes are of equal length, while the vertical axis is of different length and may be either shorter or longer than the other two.
a = b ≠ c
α = β = γ = 90°
Bravais lattice → Bravaisova rešetka
Bravais lattice is a set of points constructed by translating a single point in discrete steps by a set of basis vectors. The French crystallographer Auguste Bravais (1811-1863) established that in three-dimensional space only fourteen different lattices may be constructed. All crystalline materials recognised till now fit in one of these arrangements. The fourteen three-dimensional lattices, classified by crystal system, are shown to the bottom.
|
Crystal system
|
Bravais lattices
|
|||
|
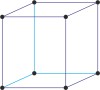
cubic a=b=c α=β=γ=90° |
 |
 |
 |
|
|
|
simple cubic
|
body-centered cubic
|
face-centered cubic
|
|
|
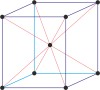
tetragonal a=b≠c α=β=γ=90° |
 |
 |
||
|
|
simple tetragonal
|
body-centered tetragonal
|
||
|
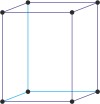
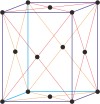
orthorhombic a≠b≠c α=β=γ=90° |
 |
 |
 |
 |
|
|
simple orthorhombic
|
base-centered orthorhombic
|
body-centered orthorhombic
|
face-centered orthorhombic
|
|
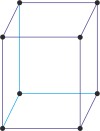
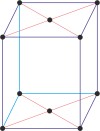
monoclinic a≠b≠c α=γ=90°≠β |
 |
 |
||
|
|
simple monoclinic
|
base-centered monoclinic
|
||
|
hexagonal a=b≠c α=β=90° γ=120° |
 |
|||
|
|
hexagonal
|
|||
|
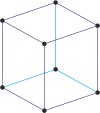
rhombohedral a=b=c α=β=γ≠90° |
 |
|||
|
|
rhombohedral
|
|||
|
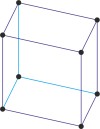
triclinic a≠b≠c α≠β≠γ≠90° |
 |
|||
|
triclinic
|
||||
crystal system → kristalni sustav
Crystal system is a method of classifying crystalline substances on the basis of their unit cell. There are seven unique crystal systems. The simplest and most symmetric, the cubic (or isometric) system, has the symmetry of a cube. The other six systems, in order of decreasing symmetry, are hexagonal, tetragonal, rhombohedral (also known as trigonal), orthorhombic, monoclinic and triclinic.
|
Crystal system
|
Unit-cell
|
Conditions on unit-cell edges and angles |
|
cubic |
 |
a=b=c α=β=γ=90° |
|
hexagonal |
 |
a≠c α=γ=90° β=120° |
|
tetragonal |
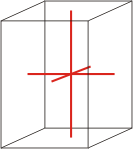 |
a=b≠c α=β=γ=90° |
|
rhombohedral |
 |
a=b=c α=β=γ≠90° |
|
orthorhombic |
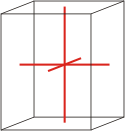 |
a≠b≠c α=β=γ=90° |
|
monoclinic |
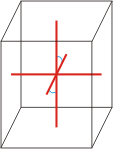 |
a≠b≠c α=γ=90°≠β |
|
triclinic |
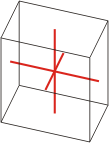 |
a≠b≠c α≠β≠γ≠90° |
Citing this page:
Generalic, Eni. "Tetragonal." Croatian-English Chemistry Dictionary & Glossary. 29 June 2022. KTF-Split. {Date of access}. <https://glossary.periodni.com>.
Glossary
Periodic Table