CHEMISTRY GLOSSARY

position vector    →   položajni vektor

The location of a point-like object relative to the origin of a coordinate system is given by a position vector r, which in unit vector notation is

where x, y and z are the scalar components of r.

Newton’s gravitational law    →   Newtonov zakon gravitacije

Every object in the universe attracts every other object with a force (gravitational force F_G) directed along the line through centres of the two objects that is proportional to the product of their masses and inversely proportional to the square of the distance between them.

m₁ and m₂ are masses of the two objects and r is the distance between them. G is universal constant of gravitation, which equals 6.67•10^-26 N m² kg^-2. Strictly speaking, this law applies only to objects that can be considered pointlike object. Otherwise, the force has to be found by integrating the forces between various mass elements.

It is more properly to express Newton’s gravitational law by vector equation:

in which r₁ and r₂ are position vectors of masses m₁ and m₂.

Gravitational forces act on distance. Newton’s gravitational law is derived from Kepler’s law for planetary motion, using a physical assumption considering Sun as the centre and the source of gravitational force.

Additionally, every object moves in the direction of the force acting on it, with acceleration that is inversely proportional to the mass of object. For bodies on the surface of Earth, the distance r in gravitational law formula is practically equal to the Earth radius, R_E. If the mass of the body on Earth surface is m and the mass of earth is M_E, the gravitational force acting on that body can be expressed as:

where g is gravitational acceleration which is, although dependent on geographical latitude, usually considered as constant equal to 9.81 m s^-2.

velocity    →   brzina

If a point-like object moves so that its position vector changes from being r_i to r_f, than the displacement Δr of object is

If a point-like object undergoes a displacement, Δr, in time Δt, its average velocity, v is defined as

The instantaneous velocity, v, is obtained from the average velocity by shrinking the time interval Δt towards zero. The average velocity approaches a limiting value, which is the velocity of a given instant:

Velocity is a vector quantity. If we plot the path of a moving particle as a curve in a coordinate system, the instantaneous velocity is always tangent to that curve.

SI unit for velocity is m s^-1.

acceleration    →   akceleracija

If a point-like object undergoes a change in velocity Δv=v_f-v_i in time Δt=t_f-t_i (indexes i and f stand for initial and final instant as well as for initial and final velocity) its average acceleration, a is defined as

The instantaneous acceleration, a, is obtained from the average acceleration by shrinking the time interval Δt towards zero. The average acceleration approaches a limiting value, which is the acceleration of a given instant:

Acceleration is a vector quantity. SI unit for acceleration is m s^-2.

base-centered monoclinic lattice    →   bazno centrirana monoklinska rešetka

Base-centered or side-centered or end-centered monoclinic lattice (monoclinic-C), like all lattices, has lattice points at the eight corners of the unit cell plus additional points at the centers of two parallel sides of the unit cell. It has unit cell vectors a≠b≠c, and interaxial angles α=γ=90°≠β.

base-centered orthorhombic lattice    →   bazno centrirana ortorompska rešetka

Base-centered or side-centered or end-centered monoclinic lattice (orthorhombic-C), like all lattices, has lattice points at the eight corners of the unit cell plus additional points at the centers of two parallel sides of the unit cell. It has unit cell vectors a≠b≠c and interaxial angles α=β=γ=90°.

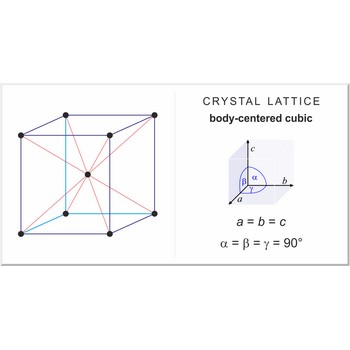
body-centered cubic lattice    →   prostorno centrirana kubična rešetka

Body-centered cubic lattice (bcc or cubic-I), like all lattices, has lattice points at the eight corners of the unit cell plus an additional points at the center of the cell. It has unit cell vectors a = b = c and interaxial angles α=β=γ=90°.

The simplest crystal structures are those in which there is only a single atom at each lattice point. In the bcc structures the spheres fill 68 % of the volume. The number of atoms in a unit cell is two (8 × 1/8 + 1 = 2). There are 23 metals that have the bcc lattice.

body-centered orthorhombic lattice    →   prostorno centrirana ortorompska rešetka

Body-centered orthorhombic lattice (orthorhombic-I), like all lattices, has lattice points at the eight corners of the unit cell plus an additional points at the center of the cell. It has unit cell vectors a≠b≠c and interaxial angles α=β=γ=90°.

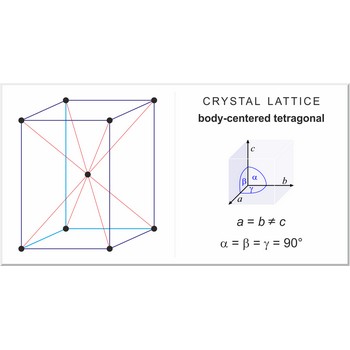
body-centered tetragonal lattice    →   prostorno centrirana tetragonska rešetka

Body-centered tetragonal lattice (tetragonal-I), like all lattices, has lattice points at the eight corners of the unit cell plus an additional points at the center of the cell. It has unit cell vectors a=b≠c and interaxial angles α=β=γ=90°.

dipole moment    →   dipolni moment

Electric dipole moment (μ) is a product of the positive charge and the distance between the charges. Dipole moments are often stated in debyes; The SI unit is the coulomb metre. In a diatomic molecule, such as HCl, the dipole moment is a measure of the polar nature of the bond; i.e. the extent to which the average electron charges are displaced towards one atom (in the case of HCl, the electrons are attracted towards the more electronegative chlorine atom). In a polyatomic molecule, the dipole moment is the vector sum of the dipole moments of the individual bonds. In a symmetrical molecule, such as tetrafluoromethane (CF₄) there is no overall dipole moment, although the individual C-F bonds are polar.